Test de Kolmogorov-Smirnov

Une fonction de répartition F d'une variable aléatoire X est définie pour tout nombre réel x, par

F(x) = P(X < x)

En d'autres termes, F(b) est la probabilité que la variable aléatoire X prenne une valeur inférieure à b. Pour un échantillon uniformément distribué entre 0 et 1, on a F(x) = x, avec x compris entre 0 et 1.

Exemple
Soit la suite ordonnée de n=10 nombres pseudo-aléatoires: 0.0582795, 0.248849, 0.326321, 0.411576, 0.435057, 0.485013, 0.5035, 0.547168, 0.611682, 0.998397. La fonction de répartition Fn(x) de cet échantillon sera (en bleu dans le graphique de gauche):


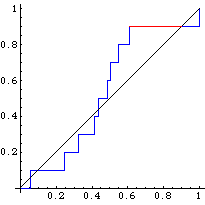10 nombres, D = 0.2883 < 0.410,
accepté (a = 5%)
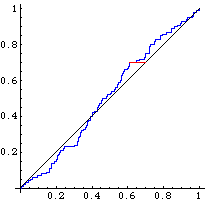100 nombres, D = 0.0833 < 0.136,
accepté (a = 5%)
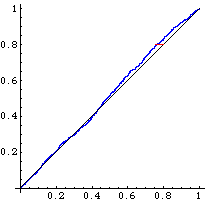1000 nombres, D = 0.0433 > 0.043,
refusé de justesse (a = 5%)

On remarque que quand n augmente, Fn(x) se rapproche de F(x).
Le test de Kolmogorov-Smirnov compare la fonction de répartition uniforme avec la fonction de répartition de l'échantillon empirique. L'idée est de calculer la distance maximale (en rouge sur les graphiques) entre les fonctions théoriques et empiriques. Si cette distance dépasse une certaine valeur, qu'on lira dans un tableau, on dira que l'échantillon est mauvais.

Méthode

On procède de la façon suivante:

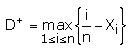  1. Générer n nombres aléatoires entre 0 et 1 et les trier par ordre croissant: X1, X2, ..., Xn.
  2. Calculer et
  3. Calculer D = max(D+, D-)

  4. Déterminer la valeur critique Da(n) dans le tableau ci-dessous.
  5. Si D > Da(n), on dit que l'échantillon est mauvais (voir tableau ci-dessous).

Taille de
l'échantillon
(n) 		Seuils critiques Da(n)
a = .20 a = .15 a = .10 a = .05 a = .01
1 .900 .925 .950 .975 .995
2 .684 .726 .776 .842 .929
3 .565 .597 .642 .708 .828
4 .494 .525 .564 .624 .733
5 .446 .474 .510 .565 .669
6 .410 .436 .470 .521 .618
7 .381 .405 .438 .486 .577
8 .358 .381 .411 .457 .543
9 .339 .360 .388 .432 .514
10 .322 .342 .368 .410 .490
11 .307 .326 .352 .391 .468
12 .295 .313 .338 .375 .450
13 .284 .302 .325 .361 .433
14 .274 .292 .314 .349 .418
15 .266 .283 .304 .338 .404
16 .258 .274 .295 .328 .392
17 .250 .266 .286 .318 .381
18 .244 .259 .278 .309 .371
19 .237 .252 .272 .301 .363
20 .231 .246 .264 .294 .356
25 .210 .220 .240 .270 .320
30 .190 .200 .220 .240 .290
35 .180 .190 .210 .230 .270
> 35 1.07 / 1.14 / 1.22 / 1.36 / 1.63 /

Exercice

Programmez en Mathematica le test de Kolmogorov-Smirnov et testez les générateurs que vous avez déjà programmés.

Fonctions Mathematica utiles: AppendTo, For, Graphics, If, Length, Line, Print, RGBColor, Show, Sort

Le fichier Mathematica complet est disponible, mais seulement pour les visiteurs autorisés!
Mot de passe :

Références

Didier Müller, 20.1.03